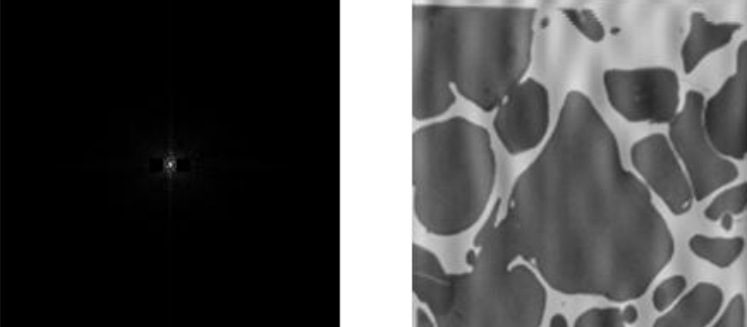
引言
3.1 傅里叶变换与离散傅里叶变换快速算法
图像的频域变换
频率通常是指一维物理量随时间变化快慢程度的度量。
例如：交流电频率为50～60Hz（交流电压）、中波某电台1026kHz（无线电波）
图像是二维信号，其坐标轴是二维空间坐标轴， 图像本身所在的域称为空间域（Space Domain）。
每一种变换都有自己的正交函数集，引入不同的变换
傅里叶变换与时频分析
人类视觉所感受到的是在空间域和时间域的信号。但是，往往许多问题在频域中讨论时，有其非常方便分析的一面。
我们知道，任何复杂的周期信号f(t)可以用简单的调和振荡函数表示成如下形式：
这就是著名的傅里叶级数， 和 都是简单的调和振荡函数，直观讲都是正弦波。 和 是函数 的傅里叶系数，可由以下公式计算：
于是，周期函数f(t) 就与下面的傅里叶序列产生了一一对应，即
从数学上已经证明了，傅里叶级数的前 项和是原函数 在给定能量下的最佳逼近：
对于L2(R)上的非周期函数f(t) ，有
称 为 的傅里叶变换，反变换公式为
当一个一维信号 满足狄里赫莱条件，即
（1） 具有有限个间断点；
（2） 具有有限个极值点；
（3） 绝对可积。
则其傅里叶变换对（傅里叶变换和逆变换）一定存在。在实际应用中，这些条件一般总是可以满足的。
一维傅里叶变换对的定义为:
式中： , 称为时域变量， 称为频域变量。
例1：
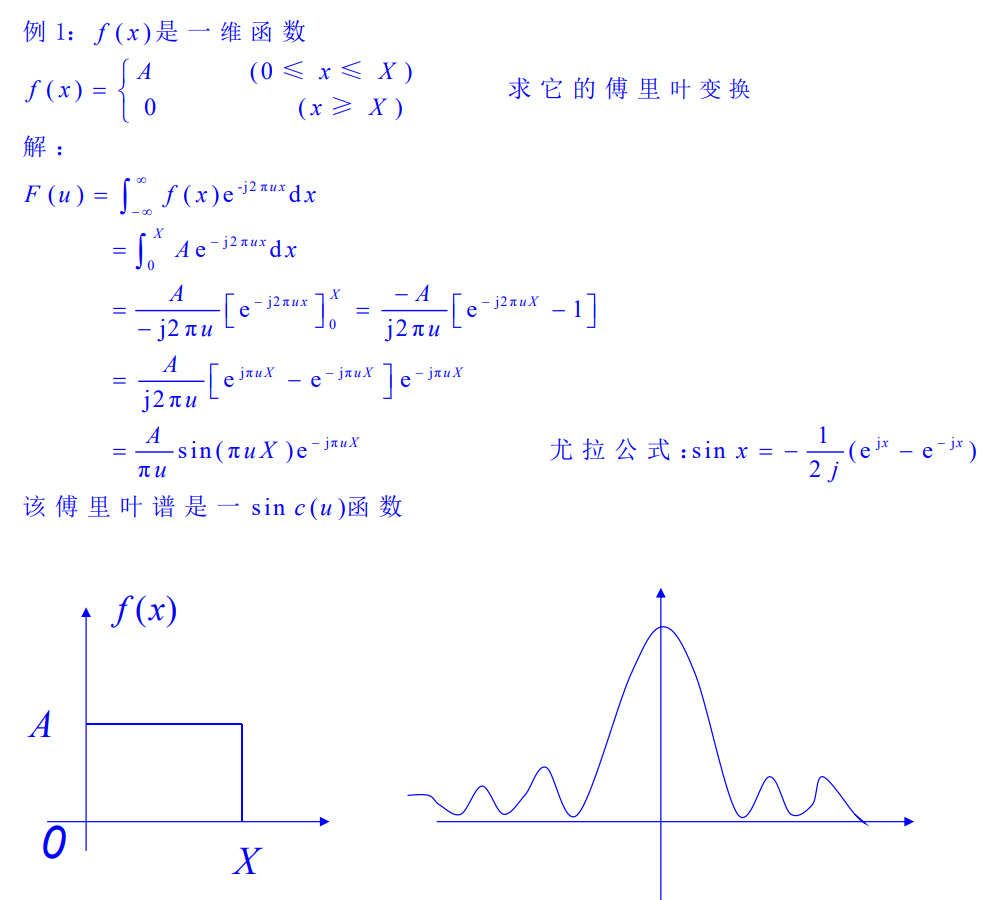
一维傅里叶变换可以很容易地推广到二维，如果二维函数 满足狄里赫莱条件，则它的二维傅里叶变换对为:
式中: 称为时域变量， 称为频域变量。
例2：
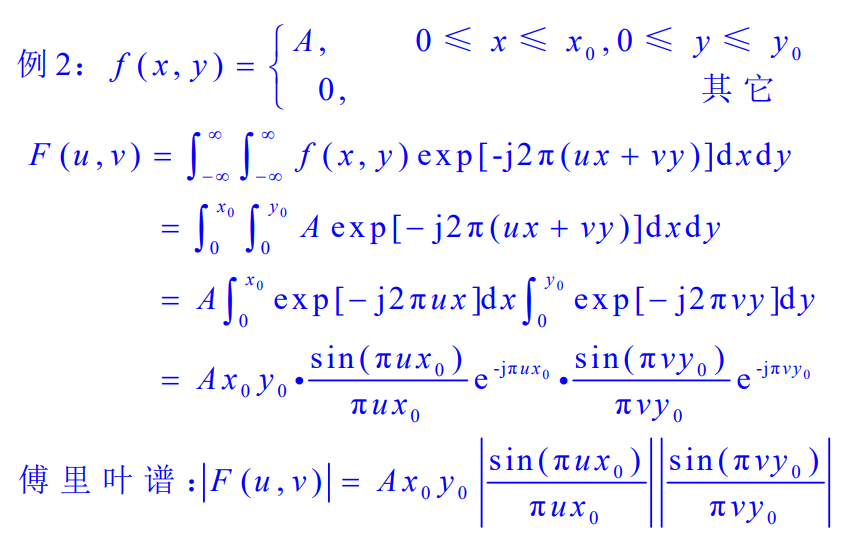
在数字图像处理中应用傅里叶变换， 还需要解决两个问题：
一是在数学中进行傅里叶变换的 为连续（模拟）信号， 而计算机处理的是数字信号（图像数据）；
二是数学上采用无穷大概念，而计算机只能进行有限次计算。
计算机能运算的傅里叶变换称为离散傅里叶变换（Discrete Fourier Transform，DFT)。
设 为一维信号 的 个抽样， 其离散 傅里叶变换对为:
(1)
(2)
式中：
注：式 （2） 中的系数 也可以放在式 （1） 中， 有时也可在傅里叶正变换和逆变换前分别乘以 ， 这是无关紧要的， 只要正变换和逆变换前系数乘积等于 即可。
由欧拉公式: (3)
将式 （3） 代入式 （1），并利用 ，可得:
(4)
可见，离散序列的傅里叶变换仍是一个离散的序列，每一个 对应的傅里叶变换结果是所有输入序列 的加权和（每一个 都乘以不同频率的正弦和余弦值）， 决定了每个傅里叶变换结果的频率。
通常傅里叶变换为复数形式， 即:
(5)
式中， 和 分别是 的实部和虚部。式 (5) 也可表示成指数形式：
其中 (7) ; (8)
通常称 为 的频谱或傅里叶幅度谱， 为 的相位谱。频谱的平方称为能量谱或功率谱，它表示为:
考虑到两个变量，就很容易将一维离散傅里叶变换推广到二维。二维离散傅里叶变换对定义为:
式中： ； ； 为时域变量， 为频域变量。
像一维离散傅里叶变换一样，系数 可以在正变换或逆变换中，也可以在正变换和逆变换前分别乘以系数 ，只要两式系数的乘积等于 即可。
Fourier变换有两个好处：
1）可以得出信号在各个频率点上的强度。
2）可以将卷积运算化为乘积运算。
图像频域处理的理论基础
卷积理论
• 被处理图像
• 变换函数 ，线性、位置无关操作
• 目标图像
有卷积：
有等式：
有等式：
傅里叶变换
利用傅里叶变换的特性，将时间信号正变换到频率域后进行处理（例如低通、高通或带通），然后再反变换成时间信号，即可完成对信号的滤波。
• 低通滤波：在频率域中抑制高频信号
• 高通滤波：在频率域中抑制低频信号
二维离散函数的傅里叶频谱、 相位谱和能量谱分别为:
(11)
(12)
(13)
式中， 和 分别是 的实部和虚部。
1.可分离性
一个二维傅里叶变换可分解为两步进行， 其中每一步都是一个一维傅里叶变换，
先对 按行进行傅里叶变换得到 ，再对 按列进行傅里叶变换，便可得到 的傅里叶变换结果，
如图所示。显然对 先按列进行离散傅里叶变换， 再按行进行离散傅里叶变换也是可行的。
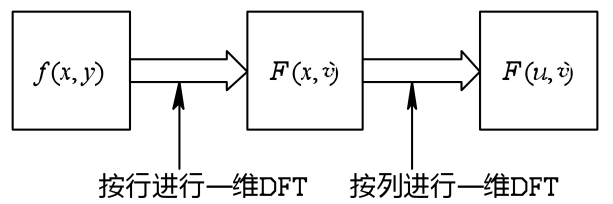
2.平移性质
图像中心化
平移性质表明，只要将 乘以因子 ，再进行离散傅里叶变换，即可将图像的频谱原点 移动到图像中心 处。如图所示：
下图是简单方块图像平移的结果：
3.旋转不变性
由旋转不变性，如果时域中离散函数旋转 角度，则在变换域中该离散傅里叶变换函数也将旋转同样的角度。离散傅里叶变换的旋转不变性如图所示。
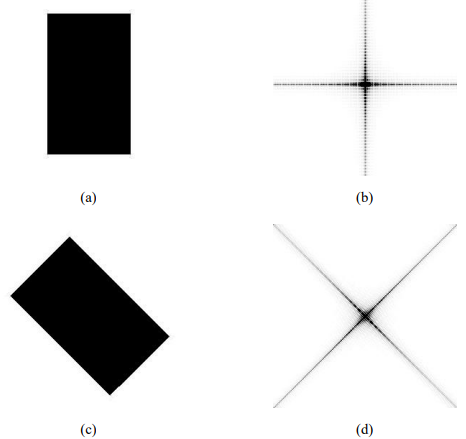
（a）原始图像 （b）原始图像的傅里叶频谱 （c）旋转 后的图像 （d）图像旋转后的傅里叶频谱
由于二维离散傅里叶变换具有可分离性， 即它可由两次一维离散傅里叶变换计算得到，因此，仅研究一维离散傅里叶变换的快速算法即可。
先将式 （1） 写为：
(14)
式中， ，称为旋转因子。
可将式 （14） 所示的一维离散傅里叶变换（DFT）用矩阵的形式表示为：
式中，由 构成的矩阵称为 阵或系数矩阵。
观察DFT的 阵，并结合 的定义表达式 ，可以发现系数 是以 为周期的、以 为对称的。这样， 阵中很多系数不必进行多次重复计算， 即:
,
因此可进一步减少计算工作量。
例如，对于 ， 阵为：
由 的周期性得： ；再由 的对称性可得： 。于是式 (15) 可变为:
可见 的W阵中只需计算 和 两个系数即可。这说明 阵的系数有许多计算工作是重复的，
如果把一个离散序列分解成若干短序列， 并充分利用旋转因子W的周期性和对称性来计算离散傅里叶变换，便可以简化运算过程，这就是FFT的基本思想。
设N为2的正整数次幂， 即：
(17)
令 为正整数，且
将式 (17) 代入式 (14)，离散傅里叶变换可改写成如下形式：
由旋转因子W的定义可知 ，因此 变 (18) 为：
(19)
现定义
(20)
, (21)
式 (19) 变为：
(22)
进一步考虑 的对称性和周期性可知 和
(23)
由此，可将一个 点的离散傅里叶变换 分解成 两个N／2短序列的离散傅里叶变换，即分解为偶数和奇数序列的离散傅里叶变换 和 。
以计算N=8的DFT为例 …… 待补充
傅里叶变换在图像处理中是一个最基本的数学工具。利用这个工具，可以对图像的频谱进行各种各样的处理，如滤波、降噪、增强等。
