知识图谱推理FOIL
归纳逻辑程序设计 (inductive logic programming,ILP)算法是机器学习和逻辑程序设计交叉领域的研究内容。
ILP使用一阶谓词逻辑进行知识表示,通过修改和扩充逻辑表达式对现有知识 归纳,完成推理任务。
作为ILP的代表性方法,FOIL(First Order Inductive Learner)通过序贯覆盖实现规则推理。
概述: 从一般到特殊, 逐步给目标谓词添加前提约束谓词, 使其覆盖所有的正例,而不覆盖任何反例
例:
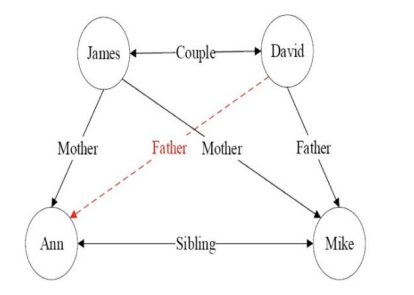
问题: 如何从知识图谱中推理得到:
father(David, Ann)
若能推理出这条规则, 问题得解.
Father(x, y)Father(David, Mike)
| 背景知识 | P的正例集合 | P的反例集合 |
|---|---|---|
| Sibling(Ann,Mile) | Father(David,Mike) | Father(David,James) |
| Couple(David,James) | Father(James,Ann) | |
| Mother(James,Ann) | Father(James,Mike) | |
| Mother(James,Mike) | Father(Ann,Mike) |
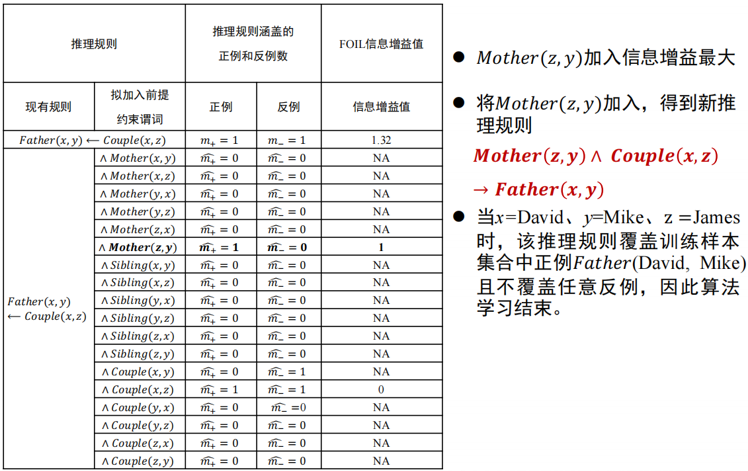
计算推理规则覆盖的正例和反例
如:
将 Monther(z, y)作为前提约束谓词加入, 可得到推理规则Monther(z, y) → Father(x, y)在背景知识中, Monther(z, y)有两个实例:Monther(James, Mike)Monther(James, Ann)对于 Monther(James, Mike)这一实例, z=James, y=MIke, 将z和y带入Father(x, y)得到Father(x, Mike). 覆盖了 : 正例Father(David, Mike)反例Father(James, Mike)Father(Ann, Mike)对于 Monther(James, Ann)这一实例, z=James, y=Ann, 将z和y带入Father(x, y)得到Father(x, Ann). 覆盖了: 反例Father(James, Ann)
计算信息增益值(information gain)

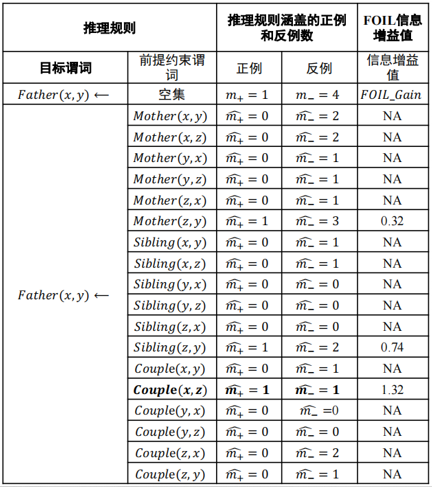
NA(Not Available): FOIL_Gain为负无穷时
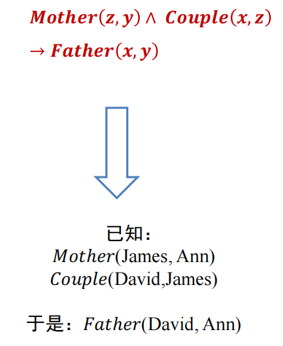
Couple(x, z)Couple(x, z)加入后信息增益最大, 将其加入推理规则, 得到Couple(x, z) → Father(x, y)
Father(x, y)中的x只能是David. 新的训练样本集如下:
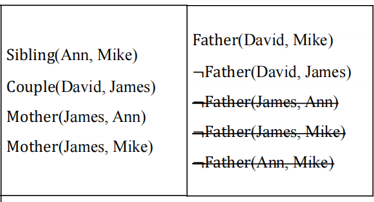
重复3 4 5步骤, 直到新规则不覆盖任何反例
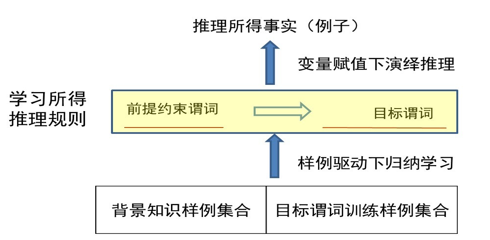
给定目标谓词,FOIL算法从实例(正例、反例、背景知识样例)出发,不断 测试所得推理规则是否还包含反例,一旦不包含,则学习结束,由此充分展 示了“归纳学习”的能力。在学得推理规则后,再给推理规则中的变量赋予具体例子,经过“演绎”得到新的知识
目标谓词P —— Father(x,y)
表格中列出该知识图谱的背景知识、正例和反例
| 背景知识 | P的正例集合 | P的反例集合 |
|---|---|---|
| Sibling(Ann,Mile) | Father(David,Mike) | Father(David,James) |
| Couple(David,James) | Father(James,Ann) | |
| Mother(James,Ann) | Father(James,Mike) | |
| Mother(James,Mike) | Father(Ann,Mike) |
target = expr('Father(x,y)')
examples_pos中
examples_neg中
from knowledge import *
A, B, C, D, E, F, G, H, I, x, y, z = map(expr, 'ABCDEFGHIxyz')
# 背景性的知识放入FOILContainer中
small_family = FOILContainer([expr("Sibling(Ann,Mike)"),
expr("Couple(David,James)"),
expr("Mother(James,Ann)"),
expr("Mother(James,MIke)"),
])
# 要推导的部分:目标谓词P
target = expr('Father(x, y)')
# P的正例部分:使用知识库中已有的三元组来构建
examples_pos = [{x: expr('David'), y: expr('Mike')}]
# P的反例部分:用否定已有确定关系的三元组的方式来构建
examples_neg = [{x: expr('David'), y: expr('James')},
{x: expr('James'), y: expr('Ann')},
{x: expr('James'), y: expr('Mike')},
{x: expr('Ann'), y: expr('Mike')}]
# run the FOIL algorithm
clauses = small_family.foil([examples_pos, examples_neg], target)
# Father(x,y)的规则体
print (clauses)
运行FOIL algorithm,给出推理结果
[[Father(x, y), [Couple(x, v_4), Sibling(v_5, y)]]]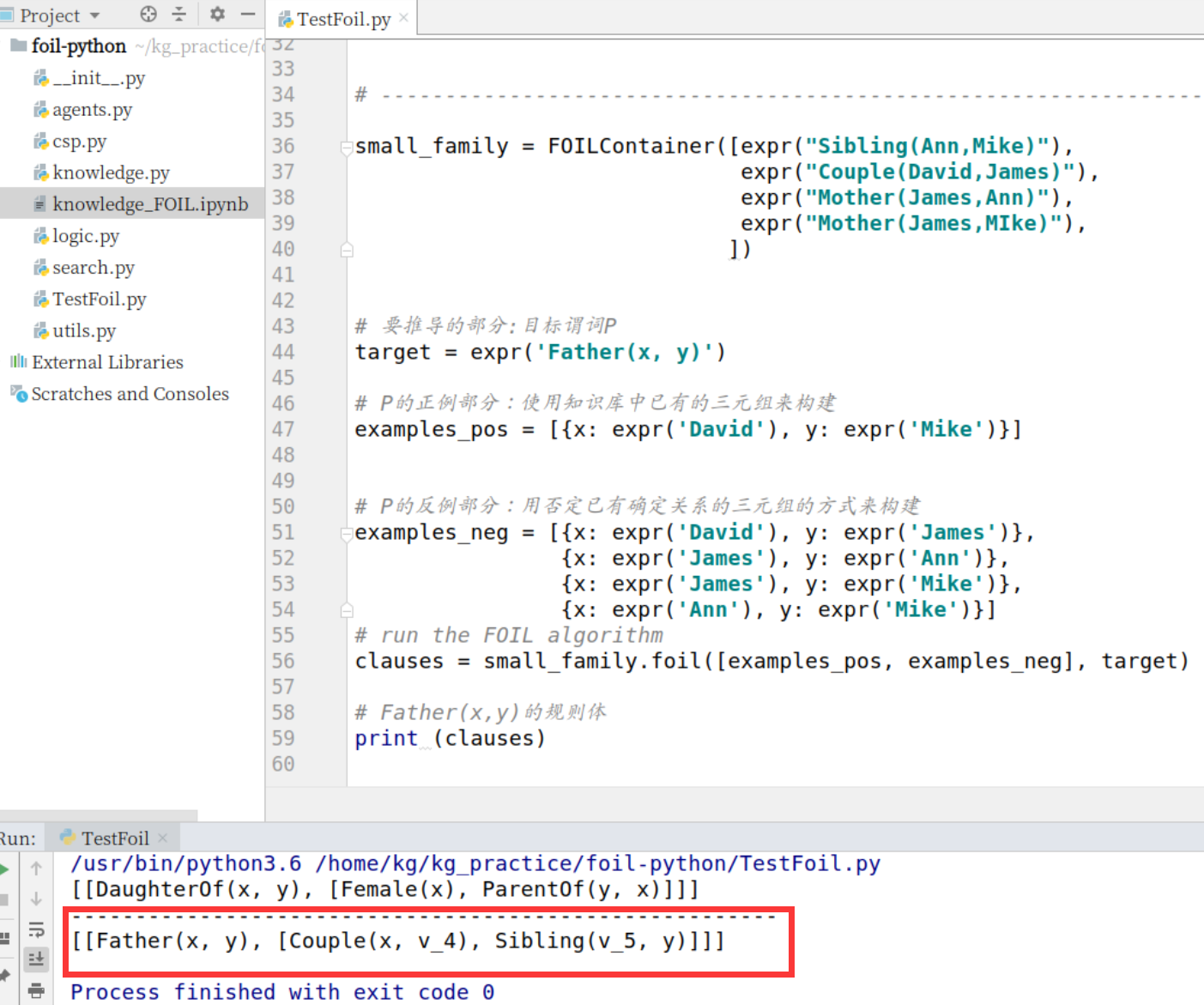
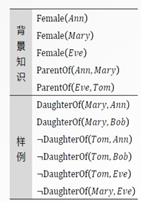
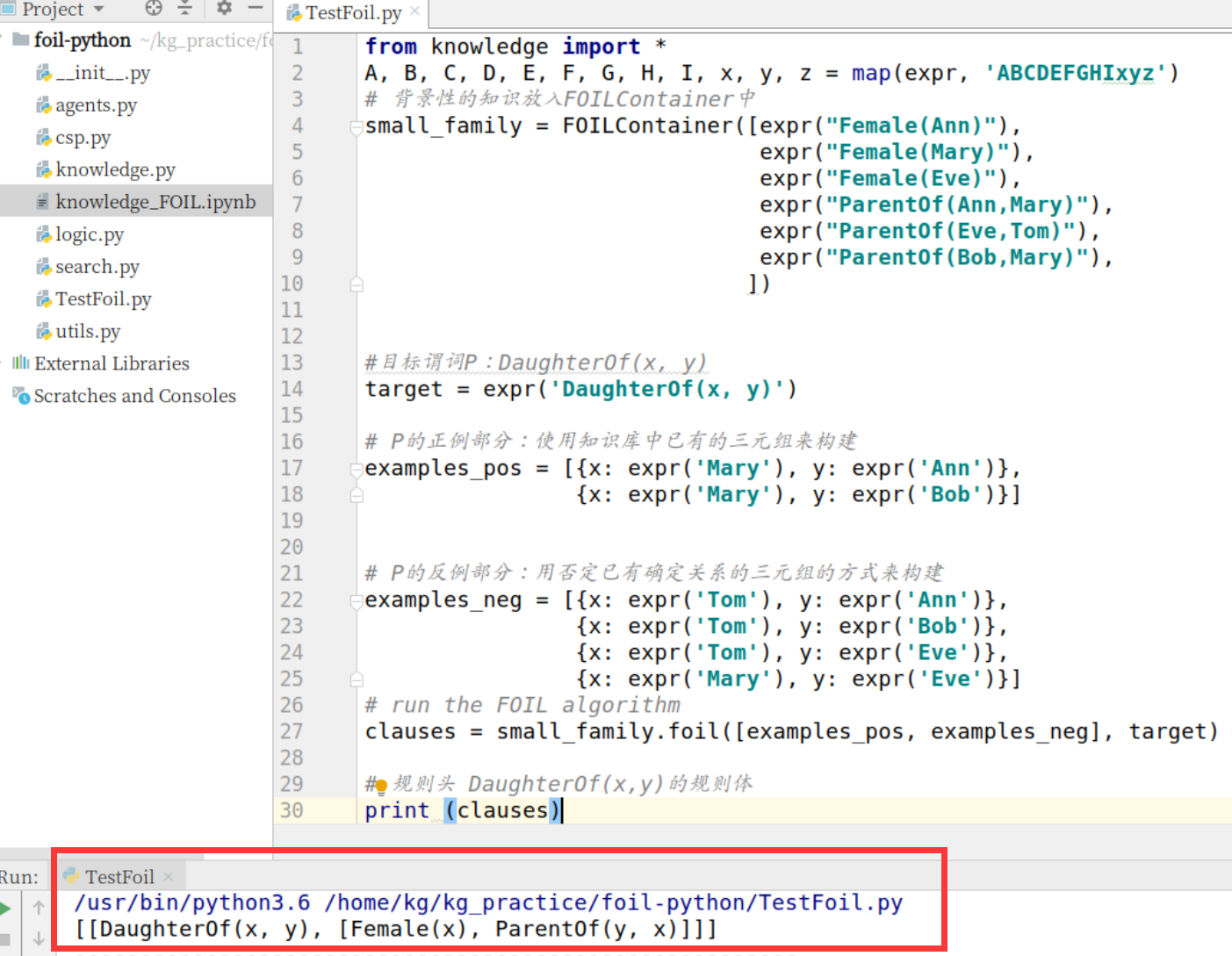
将背景性的知识放入FOILContainer中
需要注意的是,要根据已给出的正反例将背景知识补充完整,否则将推理不出结果
这里由正例DaughterOf(Mary,Bob)可知Mary是Bob的女儿,所以在背景知识中需要补充ParentOf(Bob,Mary) —— Bob是Mary的parent
目标谓词P:DaughterOf(x, y) target = expr('DaughterOf(x, y)')
将P的正例部分放入examples_pos中
将P的反例例部分放入examples_neg中
运行FOIL algorithm,给出推理结果
[[DaughterOf(x, y), [Female(x), ParentOf(y, x)]]]