
整体的思路是先解释单层感知器不能解决异或问题的原因,然后给出网络模型,手动计算一次传播过程,方便问题的理解,最后利用反向传播算法编程训练模型参数,最终解决该问题。
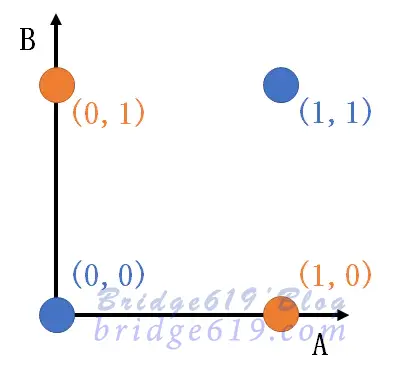
单层感知器是最简单的神经网络,由两层神经元组成,包含输入层和输出层,输入层与输出层是相连接的,输入层接受输入信号后,传递给,输出层,输出层是$M-P$神经元。单层感知器只有输出层神经元进行激活函数处理,即只有一层功能神经元,所以其学习能力是非常有限的,仅能处理 线性可分问题。而由异或问题的真值表及可视化图可以看出,异或问题是线性不可分的问题,所以一层感知机是不能解决异或问题的。
异或的真值表
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
用一个具有两个隐藏神经元和一个输出神经元结构的二层前馈神经网络来解决异或问题。
| 输入 | 训练数据集{($x_k,y_k$),k=1,2,3,4} |
|---|---|
| 1 | 网络初始化设置: |
| a) 设定$MLP$网络层数为$2$,第一层具有$2$个神经元,第二层具有$1$个神经元; | |
| b) 设定每一层神经元激活函数为$Logistic$激活函数(即$Sigmoid$激活函数); | |
| c) 设定网络的损失函数$L$,分类问题,损失函数采用交叉熵: $L_k=-y_k^T\ln\hat{y}-(1-y_k^T)\ln(1-\hat{y}_k)$ ; | |
| d) 设定学习率$\eta$和优化算法; | |
| e) 设定终止准则(精度、最大迭代次数等); | |
| f ) 网络权重初始化; | |
| 2 | 输入训练样本,前向传播,计算神经元输入$a$,输出$b$,最终输出$\hat{y}$; |
| 3 | 根据真实标签$y$与当前预期$\hat{y}$,计算各层神经元对应损失梯度$g$; |
| 4 | 利用梯度下降法,对各层连接权的权重进行更新; |
| 5 | 迭代输入训练样本,重复步骤$2$ ~ $4$ ,直到满足终止条件。 |
| 输出 | 训练收敛的MLP网络模型 |
构造的网络结构图如下:
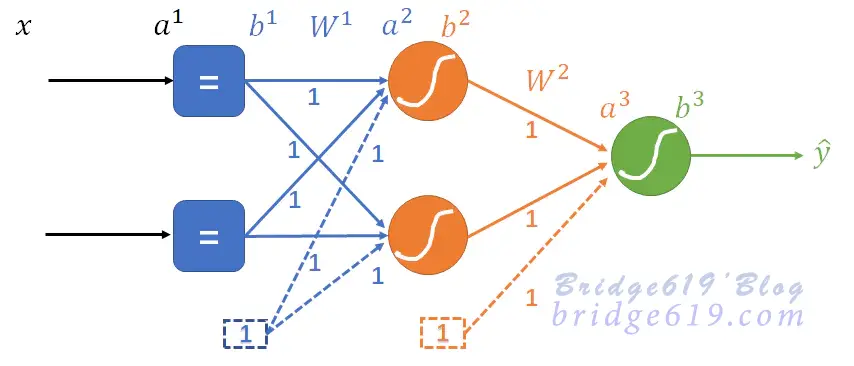
首先根据异或问题的特性构造训练样本集:
神经元的偏置均为$1$,初始化权重矩阵为:
$$W_2=\begin{bmatrix}1 & 1 & 1\end{bmatrix}$$
$x_1=[0,0]\ ,\ y_1=0$ ,前向传播过程图示及相关计算如下:

第一层:
$a^1=x_1=[0,0]^T$ ,
第二层:
第三层:
$b^3=S(a^3)=0.92$ , $\hat{y}_1=b^3=0.92$
该问题为分类问题,目标函数(损失函数)采用交叉熵: $L_k=-y_k^T\ln\hat{y}-(1-y_k^T)\ln(1-\hat{y}_k)$,
对目标函数求导$L_k'(\hat{y}_k)=\frac{1-y}{1-\hat{y}}-\frac{y}{\hat{y}}$得$e$,由$e=\frac{1-y}{1-\hat{y}}-\frac{y}{\hat{y}}$得$e_1=\frac{1-0}{1-0.92}-\frac{0}{0.92}=12.73$
$x_2,x_3,x_4$前向传播过程图示与$x_1$类似,下面不再具体给出,只给出相关计算过程。
$x_2=[0,1]\ ,\ y_2=1$
第一层:
第二层:
第三层:
由$e=\frac{1-y}{1-\hat{y}}-\frac{y}{\hat{y}}$得$e_2=\frac{1-1}{1-0.94}-\frac{1}{0.94}=-1.06$
$x_3=[1,0]\ ,\ y_3=1$
第一层:
第二层:
第三层:
由$e=\frac{1-y}{1-\hat{y}}-\frac{y}{\hat{y}}$得$e_3=\frac{1-1}{1-0.94}-\frac{1}{0.94}=-1.06$
$x_4=[1,1]\ ,\ y_4=0$
第一层:
第二层:
第三层:
由$e=\frac{1-y}{1-\hat{y}}-\frac{y}{\hat{y}}$得$e_4=\frac{1-0}{1-0.95}-\frac{0}{0.95}=20$
单样本误差的反激活:$G^3=E^3·B^3·(1-B^3)$
$g_1^3=12.73\ ·\ 0.92\ ·\ (1-0.92)\approx 0.92$
$g_2^3=-1.06\ ·\ 0.94\ ·\ (1-0.94)\approx -0.06$
$g_3^3=-1.06\ ·\ 0.94\ ·\ (1-0.94)\approx -0.06$
$g_4^3=20\ ·\ 0.95\ ·\ (1-0.95)\approx 0.95$
$G^3=[g_1^3,g_2^3,g_3^3,g_4^3]=[0.92\ \ \ -0.06\ \ \ -0.06\ \ \ 0.95]$
批处理权重梯度:
误差的反传播:$E^2=(W^{2,#})^TG^3$ 其中$W^{2,#}=W^2[:,[0,1]]$,即权重矩阵去掉偏置项,为其前两列
第二次反向激活:$G^2=E^2\ ·\ B^2\ · \ (1-B^2)$ 同上,$B^2$也应去掉偏置项
批处理权重梯度:$\Delta W^1=G^2(B^1)^T$
学习率$\eta_1=\eta_2=0.1$
更新公式:
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =[0.85315\ \ \ 0.85315\ \ \ 0.825]$
编程实现中,权值是rand函数根据给定维度生成的[0,1)之间的数据。
import numpy as np
import matplotlib.pyplot as plt
"""
构建一个隐层大小为2的二层前馈神经网络
反向传播训练模型参数
"""
# 定义sigmoid激活函数
def sigmoid(z):
return 1/(1+np.exp(-z))
# 初始化权重
def initialize_weights(n_x, n_h, n_y):
# W1 = np.array([[1,1,1],[1,1,1]])
# W2 = np.array([[1,1,1]])
W1 = np.random.randn(n_h,n_x+1)
W2 = np.random.randn(n_y,n_h+1)
weights = {"W1":W1,"W2":W2}
return weights
# 前向传播,激活函数都用sigmoid
def forward(X,wights):
W1 = wights["W1"]
W2 = wights["W2"]
B1 = np.vstack((np.transpose(X),np.ones((1,4)))) # 为训练集增加偏置
A2 = np.dot(W1,B1)
B2 = np.vstack((sigmoid(A2),np.ones((1,4)))) # 隐含层的输出
A3 = np.dot(W2,B2)
B3 = sigmoid(A3) # 输出神经元输出的结果
cache = {"B1":B1,"B2":B2,"B3":B3}
return B3,cache
# 计算损失函数,分类问题,采用交叉熵作为损失函数
def calculate_cost(B3,Y):
cost=-np.multiply(Y,np.log(B3))-np.multiply(1-Y,np.log(1-B3))
# print("c",cost)
return cost
def e(Y,cache):
B3 = cache["B3"]
return ((1-Y)/(1-B3)) - (Y/B3)
# 反向传播,计算梯度
def backword_porp(X,Y,cache,weights,cost):
B1 = cache["B1"]
B2 = cache["B2"]
B3 = cache["B3"]
W1 = weights["W1"]
W2 = weights["W2"]
E3 = e(Y,cache)
# print("E3:",E3)
# print("B3:",B3)
# 计算权重梯度dW2
G3 = np.multiply(np.multiply(E3,B3),(1-B3)) # 样本误差的反激活
# print("G3",G3)
dW2 = np.dot(G3,np.transpose(B2)) # 批处理权重梯度
# print("dW2",dW2)
# 计算权重梯度dW1
E2 = np.dot(np.transpose(W2[:,[0,1]]),G3) # 误差的反传播,权重矩阵W1应去掉偏置项
G2 = np.multiply(np.multiply(E2,B2[[0,1],:]),(1-B2[[0,1],:])) # 第二次反向激活
dW1 = np.dot(G2,np.transpose(B1)) # 批处理权重梯度
# print("dW1",dW1)
grads = {"dW1":dW1,"dW2":dW2}
return grads
# 梯度下降法更新参数
def updata_weights(weights,grads,learning_rate):
W1 = weights["W1"]
W2 = weights["W2"]
dW1 = grads["dW1"]
dW2 = grads["dW2"]
W1 = W1 - learning_rate * dW1
W2 = W2 - learning_rate * dW2
new_weights = {"W1":W1,"W2":W2}
return new_weights
# 建立BP神经网络模型
def bpnn(X,Y,n_x,n_h,n_y,num_iters,learning_rate,print_cost=False):
"""
n_x:输入层节点数
n_h:隐藏层节点数
n_y:输出层节点数
num_iters:迭代次数
learning_rate:学习率
"""
# 1.初始化参数
weights = initialize_weights(n_x, n_h, n_y)
print("迭代次数为:",num_iters)
costs = []
# 梯度下降循环
for i in range(0,num_iters):
# 2.前向传播
B3,cache = forward(X,weights)
# 3.计算损失函数
cost = calculate_cost(B3,Y)
# 4.反向传播
grads = backword_porp(X,Y,cache,weights,cost)
# 5.更新参数
weights = updata_weights(weights,grads,learning_rate)
Cost = (np.sum(cost))/4
costs.append(Cost)
# 画出损失函数的变化曲线
print("损失函数变化曲线:")
plt.figure(figsize = (20,10))
plot_x = np.arange(len(costs))
plot_y = np.array(costs)
plt.plot(plot_x,plot_y)
plt.show()
return weights
# 利用训练完的模型进行预测
def predict(X_test,new_weight):
weights = new_weight
B3,cache = forward(X_test,weights)
B3 = np.squeeze(B3) # np.squeeze(): 删除所有单维度的条目
y_pred = []
for i in range(len(B3)):
if (B3[i] >= 0.5):
B3[i] = 1
y_pred.append(int(B3[i]))
else:
B3[i] = 0
y_pred.append(int(B3[i]))
return y_pred
# 主程序
if __name__ == '__main__':
np.random.seed(200)
X = np.array([[0,0],[0,1],[1,0],[1,1]])
Y = np.array([[0,1,1,0]])
# 训练模型
train_weights = bpnn(X,Y,n_x=2,n_h=2,n_y=1,num_iters=5000,learning_rate=0.1)
print("权值:\nW1:{W1}\nW2:{W2}".format(**train_weights))
# 进行预测
X_test = X
y_pred = predict(X_test,train_weights)
# 输出预测结果
for i in range(len(y_pred)):
print("预测结果:")
print("{}XOR结果为{}".format(X_test[i], y_pred[i]))
运行结果:
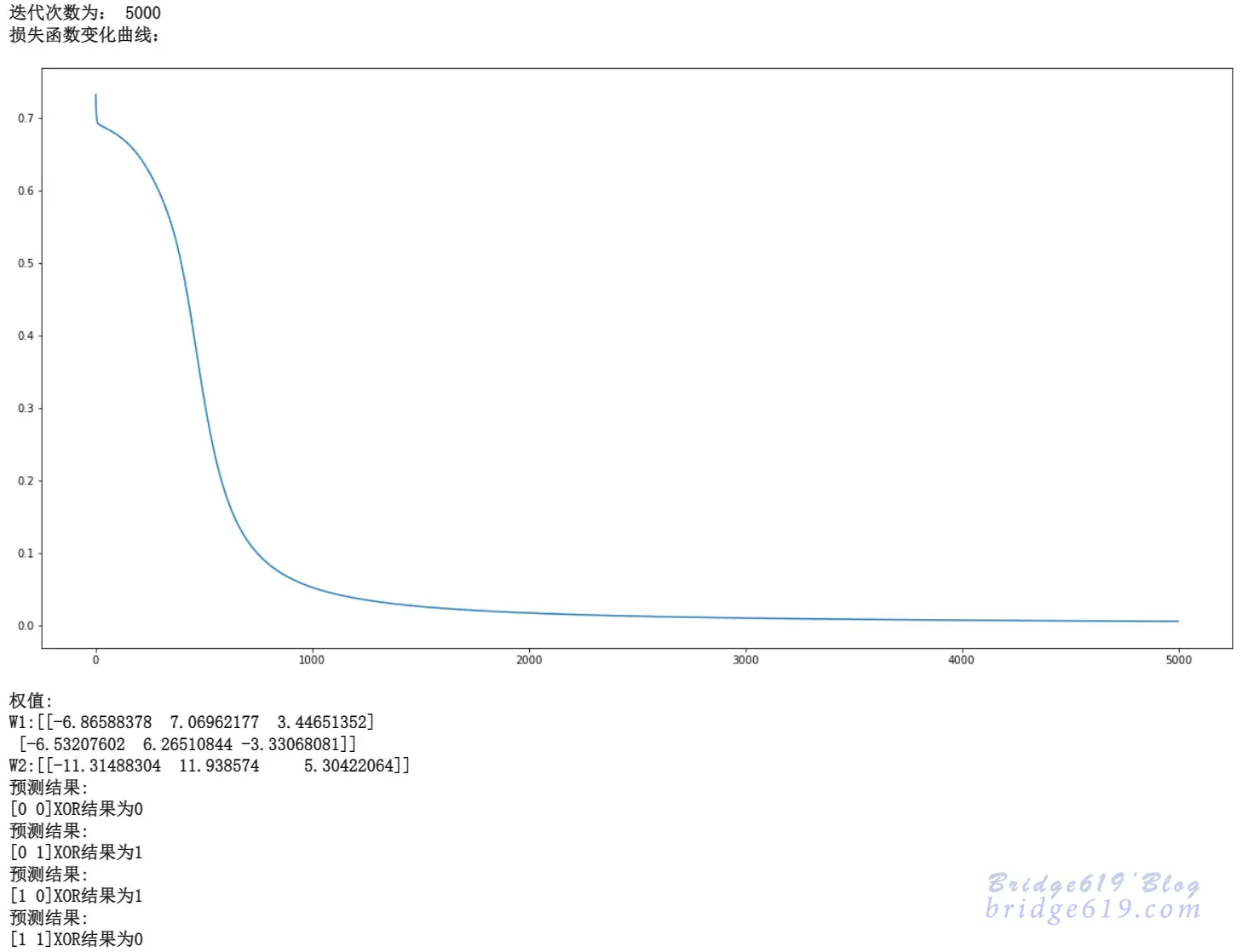
由结果可知,该模型训练成功,可以解决异或问题线性不可分的问题。