
实际情况:
①各种物理量有不同的单位和数值。例如,压力的单位为$Pa$,温度的单位为$℃$
②物理量经过$A/D$转换后变成一系列无单位的数字量。
例如,被测温度为$50$~$100 ℃$,采用$4 $ ~ $20 mA$电流传送温度模拟信号,用$8$位$A/D$转换器转换成数字量。温度、电流、数字量之间的关系如图所示:

当温度为$100℃$时,$A/D$转换器的输出为$255$;当温度为$75℃$时,$A/D$转换器的输出为$153$。
如果直接把$A/D$转换器输出的数字量显示在屏幕上,操作者不好理解。
③计算机要对物理量进行判断,显示。需要对采样数据进行标度变换。
标度变换 —— 把无单位的数字量转换成有单位的物理量。
条件: 当被测物理量与传感器或仪表的输出关系为线性关系时,采用线性变换。
变换公式为:$Y=Y_0+\frac{Y_M-Y_0}{N_M-N_0}(X-N_0)$
式中,$Y_0$ — 被测量量程的下限;$Y_m$ — 被测量量程的上限;$N_0$ — 传感器输出电压的下限;$N_m$ — 传感器输出电压的上限;$X$ — 带变换的数值;$Y$ — 变换后的数据。
例如在变送器的输出端跨接一个$250\Omega$电阻,将电流$4mA\rightarrow1V,20mA\rightarrow5V,12mA\rightarrow3V,$若$Y_m=100,Y_0=50,N_m=5,N_0=1,X=3$,则有$Y=50+\frac{100-50}{5-1}(3-1)=75℃$
条件: 传感器或变送器的输出信号与被测量之间的关系时非线性关系。
要求: 传感器的输出信号与被测信号之间的关系可以用公式表示。
例如,在流量测量中,从差压变送器来的信号$\Delta P$与实际流量$Q$成平方根关系,即$Q=K\sqrt{\Delta P}$,式中$K$ — 刻度系数,则流量的标度变换公式为:
$$\frac{Y-Q_0}{Q_M-Q_0}=\frac{K\sqrt{X}-K\sqrt{N_0}}{K\sqrt{N_m}-K\sqrt{N_0}}$$
则有:
$$Y=\frac{\sqrt{X}-\sqrt{N_0}}{\sqrt{N_m}-\sqrt{N_0}}(Q_M-Q_0)+Q_0$$
条件: 传感器输出信号与被测物理量之间的关系无法用公式表示。但是,它们之间的关系是已知的。
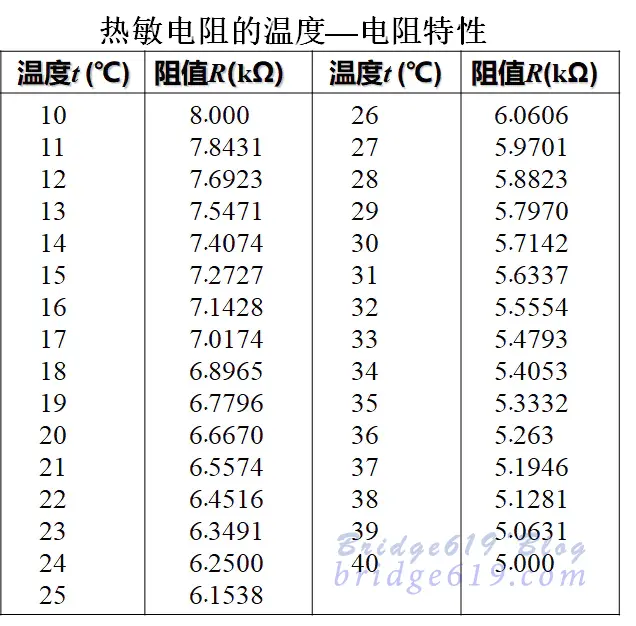
注意: 关键是找出一个较准确地反映传感器输出信号与被测量之间关系的多项式。
寻找多项式的方法:①最小二乘法 ②代数插值法
代数插值法
设被测量$y=f(x)$,传感器的输出值$x$在$n+1$个相异点$a=x_0<x_1<x_2<\ldots<x_n=b$处的函数值为
$f(x_0)=y_0,f(x_1)=y_1,\ldots,f(x_n)=y_n$,
用一个阶数为$n$的多项式$P_n(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x^1+a_0\ \ \ \ (1)$
去逼近函数$y=f(x)$,使$P_n(x)$在点$x_i$处满足:
$P_n(x_i)=f(x_i)=y_i\ \ \ \ (i=0,1,\ldots,n)\ \ \ (2)$
由于式$(1)$中的待定系数$a_0、a_1、\ldots、a_n$共有$n+1$个,而它所应满足的方程$(2)$也有$n+1$个,因此,可以得到以下方程组:
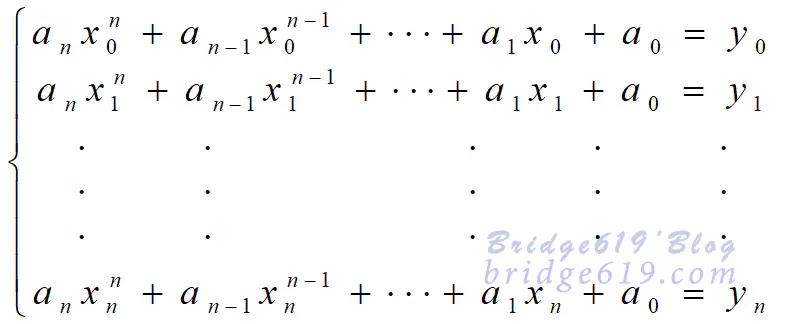
可以证明:当$x_0、x_1、\ldots、x_n$互异时,方程组有唯一的一组解。
下面以一个用热敏电阻测量温度的例子来说明这一方法的使用。
设多项式$P_n(x)$为三阶多项式$t=P_3(R)=a_3R^3+a_2R^2+a_1R+a_0$,在 热敏电阻的温度 —电阻特性表中取$t=10、17、27、39$这四点为插值点,便可以得到方程组:
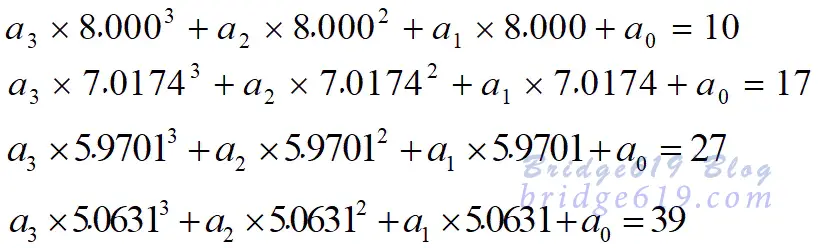
解上述方程组,得$a_3=-0.2346989\ \ \ \ a_2=6.120273\ \ \ \ a_1=-59.280430\ \ \ \ a_0=212.7118$
因此,所求的变换多项式为:$t=-0.2346989+6.120273R^2-59.28.43R+212.7118$
将采样所得到的电阻值$R$代入上式,即可求出被测温度$t$。
注意: 在函数曲线上曲率比较大的地方应适当加密插值点,这样可以得到比较高的精度。
产生的问题: 增加多项式的阶次,从而增加计算时间。
为了避免增加计算时间,经常采用表格法对非线性参数做标度变换。
表格法
指在被测量与传感器输出关系曲线上选取若干个样点,并将样点数据以表格形式存储在计算机中,对需要做标度变换的数据$y$,在其所在区间用线性插值公式:
$$y=y_i+\frac{y_{i+1}-y_i}{x_{i+1}-x_i}(x-x_i)$$
进行计算,即可完成标度变换。

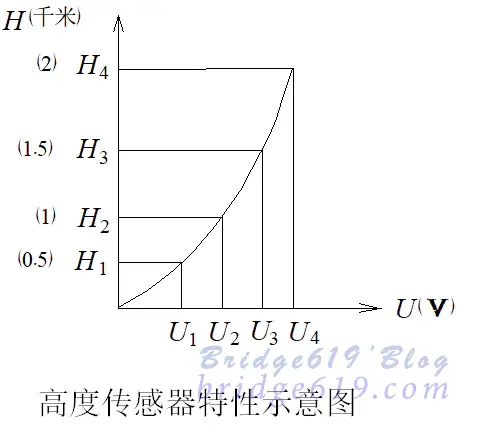
可以看出,高度和电压的关系是非线性的。很难用一个具体的函数式来表示。
要用表格法来处理。
处理方法:
将曲线分成4段,得出高度与传感器输出电压的关系式:
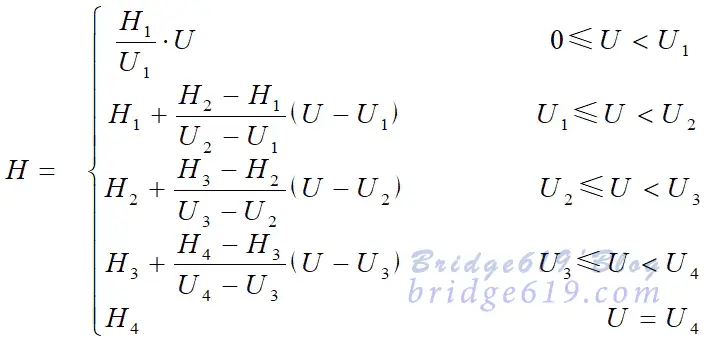
把曲线上$b$各个样点的$H_i$、$U_i$以表格形式存放在计算机
对电压$U$ 判断其所在的区间,用其所在区间关系式进行线性插值,求得对应的高度值。
数字滤波:用计算机程序对采样数据进行计算处理,减少干扰信号在有用信号中所占的比例。

中值滤波: 将$n$个采样数据进行排队,再取中间值作为本次采样值。
入口条件: $n$次采样值存在一维数组$S(n)$中。
出口条件: 滤波后的采样值存在于$DA$变量中。
中值滤波适宜去除脉动性质的干扰,不适宜快速变化的过程参数,如流量。
平均值滤波: 寻找一个$Y$作为本次采样的平均值,使该值与本次各采样值间误差的平方和最小。
$$E=\min{\sum_{i=1}^{N}e^2}=\min{\sum_{i=1}^{N}(\overline{Y}-X_i)^2}$$
由一元函数求极值原理有:
$$\overline{Y}=\frac{1}{N}\sum_{i=1}^{N}X_i$$
式中$\overline{Y}$ — $N$次采样值的算术平均值;$X_i$ — 第$i$次采样值;$N$ — 采样次数。
使用对象: 适用于对压力、流量一类信号的平滑处理。
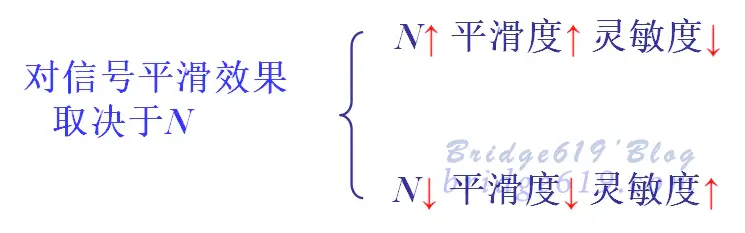
一般:流量$N=12$,压力$N=4$
用下式求平均值:
$$\overline{Y}=a_0x_0+a_1x_1+a_2x_2+\ldots+a_nx_n$$
式中$a_0、a_1、\ldots、a_n$均为常数且应满足下式:
$$\begin{cases} 0<a_0 < a_1<\ldots<a_n \ a_0+a_1+a_2+\ldots+a_n=1 \end{cases}$$
采用加权系数法选常速$a_0、a_1、\ldots、a_n$
$a_0=\frac{1}{\Delta}\ \ \ a_1=e^{-\tau}/\Delta\ \ \ \ldots \ \ \ a_n=e^{-n\tau}/\Delta$
其中$\Delta =1+e^{-\tau}+e^{-2\tau}+\ldots+e^{-n\tau}\ \ \ \ \tau:$控制对象的纯滞后时间
使用场合: 适用系统纯滞后时间常数$τ$较大、采样周期较短的过程。
优点: 对以不同采样时间得到的采样值分别给予不同的权系数,能迅速反应系统当前所受干扰的严重程度。
缺点: ①需要测试不同过程的纯滞后时间 ,②计算量大,降低了系统的处理速度。
在模拟量输入通道中,常用一阶低通$RC$滤波器来削弱干扰。
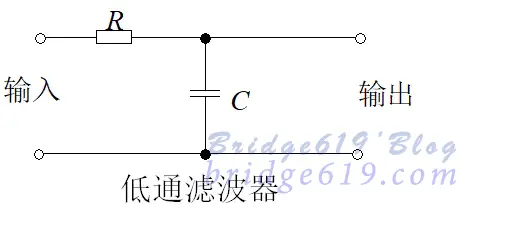
不宜用这种模拟方法对低频干扰进行滤波。原因是大时间常数、高精度的$RC$不易制作 。当 $τ↑$ ,要求$R↑$,则漏电流$↑$。可使用惯性滤波法。
惯性滤波: 以数字形式实现低通滤波的动态滤波方法。
使用场合: 滤波常数要求大。
复合滤波:先用中值滤波处理因脉冲干扰而有偏差的采样值,再把滤波后的采样值做算术平均。
复合滤波法原理可用下式表示:
若$x_1\leq x_2 \leq\ldots\leq x_N\ \ \ \ (3\leq N\leq 5)$
则$Y=(x_2+x_3+\ldots+x_{N-1})/(N-2)$
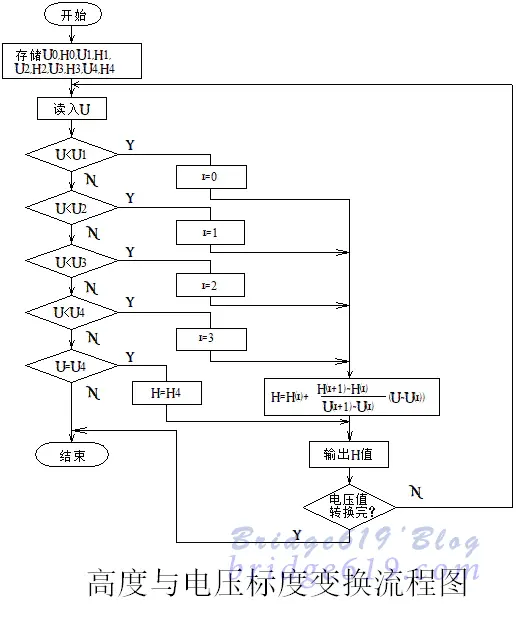
复合滤波法流程图,如图所示。
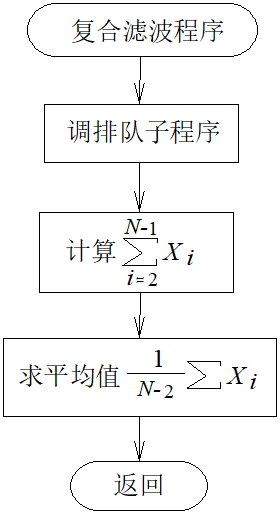
优点: 既可以去掉脉冲干扰,又可对采样值进行平滑处理。
缺点: 计算时间稍长。
在高、低速数据采集系统中,它都能削弱干扰,提高数据处理质量。
值得说明的是: 要根据实际情况正确选择数字滤波方法。
如在自动调节系统中,不恰当地采用数字滤波会把偏差值滤掉,使系统失去调节作用。
一定要根据实验来确定,千万不要凭想象行事。
采样数据中的奇异项 —— 采样数据序列中有明显错误(丢失或粗大)的个别数据。这些奇异项的存在,会使数据处理后的误差大大增加。
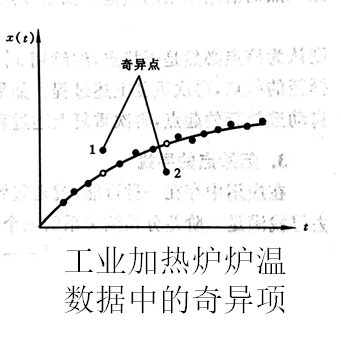
判断奇异项的准则是:
给定一个误差限$W$,若t时刻的采样值为$x_t$,预测值为$x_t'$ ,当$|x_t-x_t'|>W$时,则认为此采样值为奇异项,应予以剔除,而以预测值$x_t'$取代采样值$x_t$。
预测值$x_t'$可用以下一阶差分方程推算:$x_t'=x_{t-1}'+(x_{t-1}-x_{t-2})$
一般误差限$W$的大小要根据数据采集系统的采样频率、被测物理量的变化特性来决定。
在连续检测出若干奇异项,并用预测值替代后,必须重修选择新的$x_{i-1}$和$x_{i-2}$的值,为此,在连续替代两个奇异项之后,对以后的点,均要再加以判断,看是否满足式$(3)$:
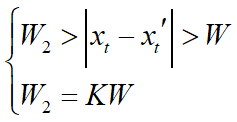
$K$值视情况而定。经验证明,一般取$K=5$较好。如果满足上述关系,则不剔除该点而沿用原来的数据。如果该点满足下式:$|x_t-x_t'|\geq W_2\ \ \ (4)$,则认为该点必然是干扰点,继续用$x_t'$取代$x_t$。
一旦找到$|x_t-x_t'|\leq W$的点就应该自动的选择新的起点,再次重复上述过程。如果找不到这一点,只要连续处理的点数已达到$6$个点,也自动选择新的起点,再次重复上述过程。
在应用中存在一种可能,就是起始点恰恰是被干扰产生的奇异点。因此,一开始就必须先去寻找满足一阶差分预测关系的三个连续点,即满足下式:
$|x_t-x_{t-1}-x_{t-1}+x_{t-2}|$
这时所找到的三个点$x_{t-1}、x_{t-2}、x_t$,可以做为正确的起始点。以$x_{t-1}$和$x_{t-2}$为起始点,往$x_1$方向预测$x_{t-3}'$,即
$x_{t-3}'=x_{t-2}+t_{t-2}-x_{t-1}$
然后根据准则,判断采样值$x_{t-3}$是否为奇异项,若为奇异项且非连续替代两次以上,则用预测值$x_{t-3}'$代替$x_{t-3}$,若是奇异项且连续替换两次以上,则按照公式$(3)\ \ \ (4)$决定是否替代;若不是奇异项则不替代。
当判断完$x_1$后,再返回到$x_{t-1}$和$x_t$处,以这两点为起始点,往$x_n$方向预测$x_{t+1}'$,即$x_{t+1}'=x_t+x_t-x_{t-1}$
再依据准则,判断采样值$x_{t+1}$是否为奇异项,若为奇异项且非连续替代两次以上,则用预测值$x_{t+1}'$代替$x_{t+1}$,若是奇异项且连续替代两次以上,则按照式$(3)\ \ \ (4)$决定是否替代;若不是奇异项则不替代。
如果$x_1、x_2、x_3$就是满足关系的连续三个点,则直接选$x_2$和$x_3$为起点,往$x_n$方向判别。
采集数据中通常会叠加噪声,噪声通常分为两大类:一类为周期性,另一类为不规则的。
为了消除干扰的影响,提高曲线的光滑度,常常需要对采样数据进行平滑处理。常用的平滑处理方法有:平均法、五点三次平滑法和样条函数法等。下面仅就平均法和五点三次平滑法讨论数据的平滑处理。
计算公式为:$y(t)=\frac{1}{2N+1}\sum_{n=-N}^{N}h(n)x(t-n)$
式子又称为$2N+1$点的简单平均。当$N=1$是为$3$点简单平均,当$N=2$时为$5$点简单平均。将式子看成一个滤波公式,则绿波因子为:
$$h(t)=(h(-N),\ldots,h(0),\ldots,h(N))$$
$$=(\frac{1}{2N+1},\ldots,\frac{1}{2N+1},\ldots\frac{1}{2N+1})$$
$$\frac{1}{2N+1}(1,\ldots,1,\ldots,1)$$
取滤波因子$h(t)=(h(-N),\ldots,h(0),\ldots,h(N))\ \ \ \ \sum_{n=-N}^Nh(n)=1$
用$h(t)$对$x(t)$进行滤波得:$y(t)=h(n)x(t)=\sum_{n=-N}^Nh(n)x(t-n)$
上式子称为$2N+1$点的加权平均公式,$y(t)$称为$x(t)$的加权平均。也常将$y(t)$称为$x(t)$与$h(t)$的卷积。
对自变量$x$按等间隔$\Delta x$采样,采集得离散数据如下:
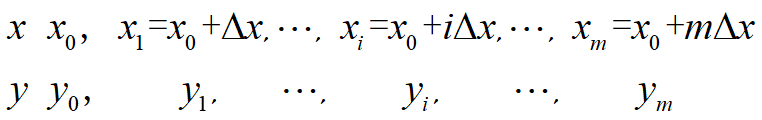
令$t=\frac{x-x_i}{\Delta x}$,上述数据变为:
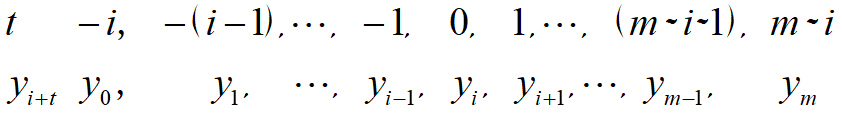
利用最小二乘法原理对离散数据进行线性平滑的方法,即为直线滑动平均法。其计算公式如下。
三点滑动平均(N=1)
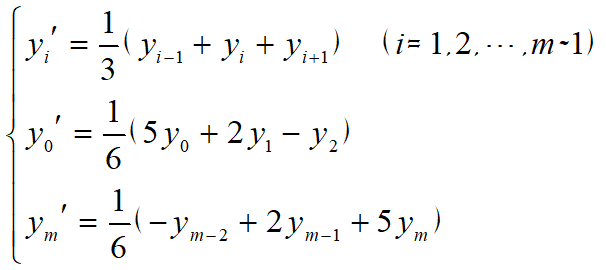
式中$y_i'$的滤波因子为$h(t)=(h(-1),h(0),h(1))=(0.333,0.333,0.333)$
五点滑动平均(N=2)
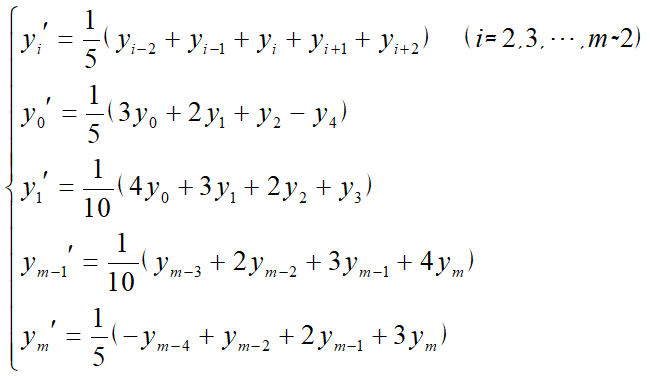
式中$y_i'$的滤波因子为$h(t)=(h(-2),h(-1),h(0),h(1),h(2))=(0.20,0.20,0.20,0.20,0.20)$
对采集到的离散数据序列$x(nT_s)$进行平滑,设采样得到的$2N+1$个间隔点$x_{-N},x_{-N+1},x_{-N+2},\ldots,x_{-2},x_{-1},x_{0},x_1,x_2,\ldots,x_{N-2},x_{N-1},x_N$上的采样值为$y_{-N},y_{-N+1},y_{-N+2},\ldots,y_{-2},y_{-1},y_{0},y_1,y_2,\ldots,y_{N-2},y_{N-1},y_N$。
设$h$为等间隔采样的步长,做变换$t=\frac{x-x_0}{h}$,则上述等间隔点变为$t_{-N}=-N,t_{-N+1}=-N+1,t_{-N+2}=-N+2,\ldots,t_{-2}=-2,t_{-1}=-1,$
$t_{0}=0,t_1=1,t_2=2,\ldots,t_{N-2}=N-2,t_{N-1}=N-1,t_N=N$。
假设用$m$次多项式$y(t)=a_0+a_1t+\ldots+a_mt^m\ \ \ (5)$来平滑所得到的采样值,为了确定出式子中的系数$a_j(j=0,1,\ldots,m)$,使多项式对于所给的采样离散值具有很好的平滑,将所有点$(t_i,y_i)$代入上式,有$2N+1$个等式:
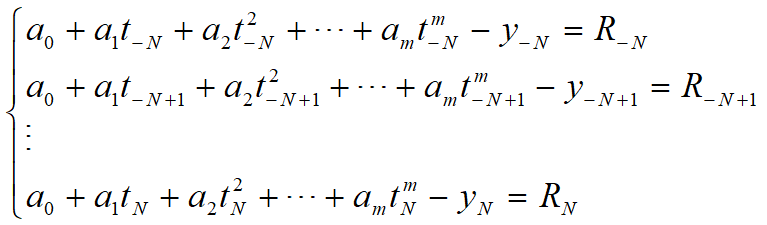
由于平滑的曲线不一定通过所有的点$(t_i,y_i)$,所以这些等式不全为$0$,根据最小二乘法原理,对于$(2N+1)$组数据$(t_i,y_i)$,求其最好的系数值$a_j$,就是求能使误差$R_i$的平方和为最小值的那些$a_j$值。
设:
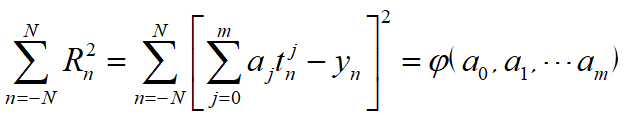
使得$\varphi(a_0,a_1,\ldots,a_m)$达到最小值。则$a_0、a_1、\ldots、a_m$必须满足下列方程:
$$\frac{\vartheta \varphi}{\vartheta \varphi}=2\sum_{n=-N}^{N}(\sum_{j=0}^{m}a_jt_n^j-y_n)t_n^k=0 \ \ (k=0,1,\ldots,m)$$
或
$$\sum_{n=-N}^{N}y_nt_n^k=\sum_{j=0}^{m}a_j\sum_{n=-N}^{N}t_n^{k+j}$$
上式叫作“正规方程组”。
当$N=2,m=3$时,并注意$N$与$t_i$的关系,则有:
$$\begin{cases} 5a_0+10a_2=y_{-2}+y_{-1}+y_0+y_1+y_2 \ 10a_1+34a_3=y_1-y_{-1}+2(y_2-y_{-2}) \ 10a_0+34a_2=y_1+y_{-1}+4(y_2+y_{-2}) \ 34a_1+130a_3=y_1-y_{-1}+8(y_2-y_{-2}) \end{cases}$$
由上面的正规方程式解出$a_0、a_1、a_2、a_3$,再代入式子$(5)$,并令$t=0、\pm1、\pm2$,得五次三次平滑公式:
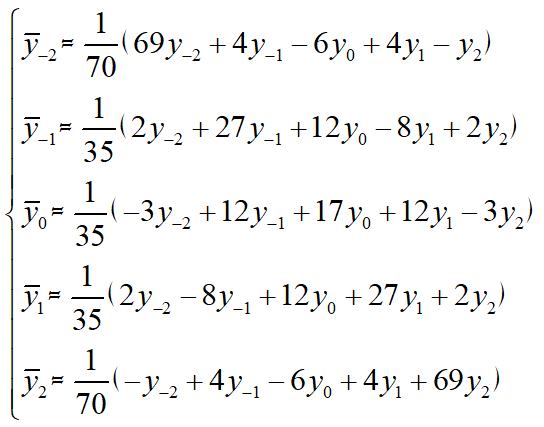
当点数很多时,为对称起见,除起始两点用上式$1$和$2$公式,末尾两点用$4$和$5$公式外,中间各点均用$3$公式进行平滑。这就相当于在每个子区间用不同的三次最小二乘多项式进行平滑。
因为在数据采集系统中,数据序列多是以$n=1、2、\ldots、N$的次序排列的,为了统一起见,将上式变为:
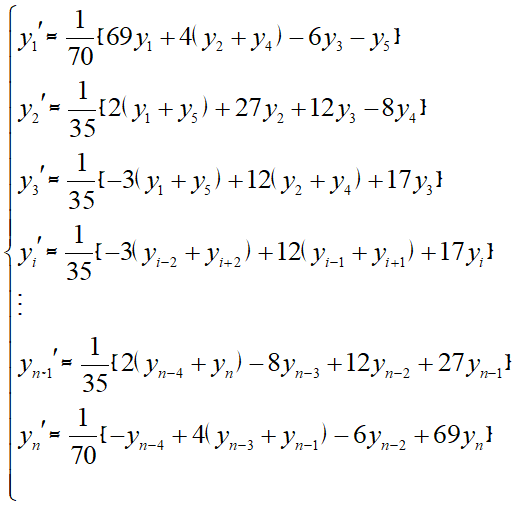
式中$y_i'$的滤波因子为:
$h(t)=(h(i-2),h(i-1),h(i),h(i+1),h(i+2))=(0.0857,0.3429,0.4857,0.3429,0.0857)$